Author: Ishita Roy
1. Abstract:
An accurate forecast of product sales is vital for the smooth operation of modern supply chains. Demand forecast helps the despatch and operations planning team predict the future market, plan the production schedule and plan inventory allocation. Therefore, planning teams needs an interactive & intelligent forecasting application to reduce supply uncertainty and anticipate change in the market. Complete end-to-end digitisation in the forecasting process creates the opportunity for enabling granular level and real-time reviews and action planning, thereby creating a chance to do actions planning & PDCA (Plan-Do-Check-Act) at a significantly rapid pace. This article will describe the process and architecture of demand forecasting for a 2-way hierarchically structured network using Hierarchical time series with ensemble techniques. The given network jointly observes hierarchy at the geographical level and product level. This article explains how the historical sales patterns are consumed to run through multiple time series models to generate future demand preserving the structural correlation among the geographical and product-level hierarchy. In the following article, we will share the details of the forecast application built by the Data Science team using Dash Plotly and code base.
2. Forecasting Method:
2.1 Problem Statement:
A significant part of TVS Motor Company's two-wheeler domestic sales and despatch planning process was managed manually with limited digitisation and without AI/data-based decisions for deriving plans. The planning team generated demand forecasts at different levels of product and geographical hierarchy based on their experience. This process was extremely time consuming and less productive. The demand forecast developed by the planning team goes through multiple levels of validation and adjustments by planning teams, Area Managers, Territory Managers and Dealerships within the network. This manual adjustment makes the forecasted numbers incoherent among the hierarchy. Therefore, the requirement was to generate systematic monthly and weekly coherent demand forecasts for all location & product combinations by considering all possible retail driving factors and providing flexibility to revise the forecast numbers preserving the hierarchical relationship. An example of a few of the retail driving forces that influence retail demand is area-specific festivals, crude oil production, the price movement of diesel, unprecedented events, unemployment index etc.
The location & product combination is given below:
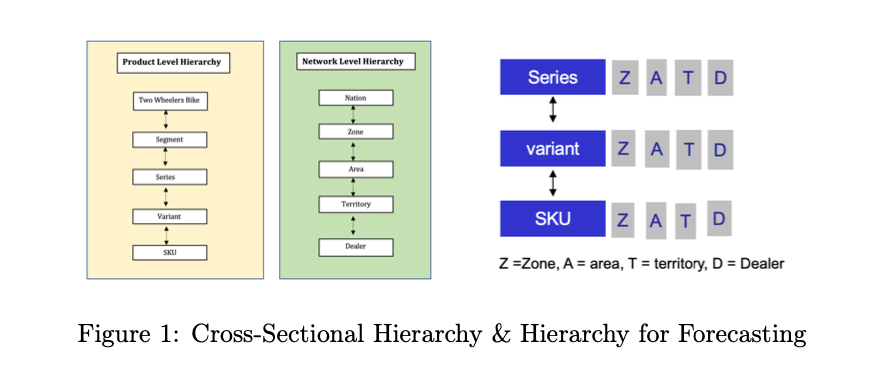
Introduction:
A hierarchical time series is a collection of time series organised in a hierarchical structure that can be aggregated at different levels (Hyndman & Athanasopoulos, 2018). Forecasts of the individual series are coherent when they sum up correctly across the levels preserving the hierarchical structure.
For example:
Figure 2 shows a 2-level hierarchical structure. At the top of the hierarchy is the Area (level 0), the most aggregate level of the data. The retail at Area at tth time point is denoted by Y_(Area,t) (t= 1, 2,..,T).
The area is divided into two territories such as T1 and T2, at level 1. The territories are further divided into two & three series at the bottom level of the hierarchy.Y_(j,t) denotes the retail time series at time point t for node j. Therefore, Y_(T1,t) denotes the tth observation of the series corresponding to node T1 at level 1 and Y_(T1D1, t) corresponds to node T1D1 and so on. In this hierarchy, we have a total of 8 (1+2+2+3) time series.
For any time point t, the observations at the bottom level of the hierarchy will sum to the observations of the series above. For example,
〖 Y〗_(Area,t) = 〖 Y〗_(T1,t) + 〖 Y〗_(T2,t) = 〖 Y〗_(T1D1,t) + 〖 Y〗_(T1D2,t)+ 〖 Y〗_(T2D1,t) + 〖 Y〗_(T2D2,t) + 〖 Y〗_(T2D3,t)
〖 Y〗_(T1,t) = 〖 Y〗_(T1D1,t) + 〖 Y〗_(T1D2,t)
〖 Y〗_(T2,t) = 〖 Y〗_(T2D1,t) + 〖 Y〗_(T2D2,t) + 〖 Y〗_(T2D3,t)
These equations can be thought of as aggregation constraints or summing equalities.
2.3 Different Types of Hierarchy:
Two distinct types of hierarchy can be observed in transactional data:
• Cross-Sectional Hierarchy: Example- In the two-wheeler automobile industry, two-wheelers are divided into categories such as commuter, moped, scooter etc. Therefore, category level retail sums up to total two-wheeler retail
• Temporal Hierarchy: Example - Weekly bike retail aggregates to monthly level sales of bikes. Again, monthly level retail sums up to yearly retail
2.4 Proposed Solution:
Hierarchical time series forecasting generates coherent forecasts that allow individual time series to be forecasted individually but preserve the relationships within the hierarchy. For individual time series at different granularities, we can build multiple time series models such as ARIMA (Autoregressive Integrated Moving Average), Holt- Winter, Prophet, ARCH (Auto Regressive Conditional Heteroscedasticity), GARCH (Generalized Autoregressive Conditional Heteroskedasticity) or ensemble models based on the EDA (Exploratory data analysis). The proposed solution is HTS Middle-out approach with ensemble techniques, starting from the Area-series level. Area-series level forecast would be disaggregated to generate territory-series, dealer-series etc., level forecasts and aggregated to generate zone-series etc., level forecasts.
2.4.1 The architecture of HTS forecasting with ensemble techniques:


In the diagram, 〖 F〗_(j,t) denotes the retail forecast series at time point t for node j. Using 〖 Y〗_(j,t) and HTS forecasting method, the forecast 〖 F〗_(j,t) are generated in such a way that the following constraints are satisfied:
〖 F〗_(Area,t) = 〖 F〗_(T1,t) + 〖 F〗_(T2,t) = 〖 F〗_(T1D1,t) + 〖 F〗_(T1D2,t)+ 〖 F〗_(T2D1,t) + 〖 F〗_(T2D2,t) + 〖 F〗_(T2D3,t)
〖 F〗_(T1,t) = 〖 F〗_(T1D1,t) + 〖 F〗_(T1D2,t)
〖 F〗_(T2,t) = 〖 F〗_(T2D1,t) + 〖 F〗_(T2D2,t) + 〖 F〗_(T2D3,t)
2.5 Benefits of HTS:
• The forecast can be generated at the lowest level of the hierarchy, and no information is lost due to aggregation
• Users have visibility of forecast numbers for all hierarchical nodes. Users can adjust forecast at any node, and subsequent impact can be easily determined hierarchically related nodes
2.6 Drawbacks of HTS:
• HTS forecasting does not allow the relationships between the series. For example, Forecast for Area 1 does not consider the forecast for Area 2 and vice versa
• It is a computationally heavy method
• Hierarchical Data preparation is the vital part of this method. To run HTS process successfully, hierarchies are needed to be determined properly
2.7 Future Scopes of Proposed Solution:
• The ensemble techniques can include many more advanced time series models
• Currently, each input time series fits each time series model (e.g., ARIMA, Holt-Winters Model) sequentially for the ensemble part. This contributes to increasing the run time. In future, we will try to fit the model parallelly
2.8 Next Article
The upcoming article will describe the architecture of forecasting application and their use. We will also share the code base for 2-way hierarchical time series forecasting with ensemble Techniques
References:
1. Forecasting: Principles and Practice (2nd ed) by Rob J Hyndman and George Anthanasopoulos. https://otexts.com/fpp2/hts.html
2. Hierarchical Time-series Models for Forecasting Oilseeds and Pulses Production in India by Dipankar Mitra, Ranjit Kumar Paul and Soumen Pal- http://ndpublisher.in/admin/issues/EAv62n1n.pdf
3. Forecasting Hierarchical Time Series in Power Generation - https://www.researchgate.net/publication/343083231_Forecasting_Hierarchical_Time_Series_in_Power_Generation


WHERE CAN I FIND THE CODE BASE?